In our group, a wide range of topics are studied with keywords of nonlinearity,
non-equilibrium, fluctuation, topology, complexity, information,
statistical analysis, and estimation. Below, the research topics by Shin-ichi Sasa,
Sigeru Shinomoto, Michikazu Kobayashi, and Hiroki Ohta are described.
Toward understanding order
(Shin-ichi Sasa)
|
The basic motivation of research is to fill in the gap between simple fundamental
law behind natural phenomena and phenomena at hand. With keeping the ultimate goal
of understanding the appearance of life and cognition as a natural phenomenon from
the standpoint of the physical law, we discuss the relationship between the
macroscopic laws of phenomena such as flow and the microscopic dynamics law
molecules and propose new phenomena. We also explore the possibility of actually
creating a system that is difficult to construct, and we study biological
functions based on physics.
|  |
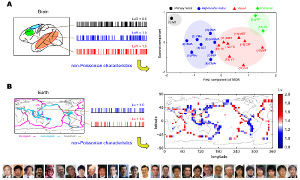
Analyzing and predicting time series of events
|
Science and technology are undergoing drastic changes in their style from
speculation to demonstration. In this era of advanced information, we are expected
to have an ability to collect detailed information, select models for grasping the
evidence, and predict their future. We are laying the foundation for such modeling
and application, in particular pertaining to time series of point events,
including neuronal spike trains or social and economic events.
|  |
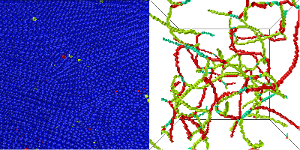
Topology in ordered state
|
Topology is an important key role to understand ordered states such as those below
phase-transition temperatures. We are studying a relationship between them such as
how the universality class of the phase transition is determined by the topology
of the system, how we can classify topological objects in ordered states such as
Nambu-Goldstone modes and topological defects, and their applications to highly
nonequilibrium physics like turbulence. Right figures show a snapshot of a
numerically obtained 3-dimensional colloidal crystal (left) and positions of
non-Abelian disclinations (right). Dynamics of disclinations are dynamically
tangled in a topologically determined manner, showing novel properties of the
nonequilibrium colloidal crystals.
|  |
Collective dynamics of many-body systems
|
The aim of my works is to find out mathematical expression for understanding how
interacting many elements lead to emergent collective behaviors in various
conditions. The core of my works include disordered systems or contact processes on
random graphs with emphasis on phase transitions, percolation, or bifurcation. A
challenging direction, for me, branched from such a motivation is mathematical
modeling of cell biology, which provide new insights to biological experiment.
|
