We are mainly interested in physics of quantum many-body systems, such as electrons in solids and ultracold atoms, which emerges as a consequence of complex correlations among the many constituent particles (electrons or atoms). Although the equation of motion for the constituent particles is explicitly written, this does not necessarily mean that we understand non-trivial properties, effects, and phenomena observed in the quantum systems with a vast amount of degrees of freedom. P. W. Anderson, who was awarded the Nobel prize in physics in 1977, appropriately phrased this situation as “More is different”. In particular, when the systems are cooled below the quantum-degeneracy temperature, natures specific to quantum mechanics, such as quantum statistics of the particles (Bose-Einstein or Fermi-Dirac statistics) and the phase of the wave function, give rise to a lot of counter- intuitive effects. Furthermore, recent experimental advances in artificial quantum platforms, including ultracold atoms, trapped ions, and superconducting circuits, have opened up new possibilities for studying quantum many-body physics under direct control of several important parameters. We aim to understand and pioneer rich physics of such quantum many-body systems by using and developing quantum field theory, large-scale numerical simulations, and quantum-information approaches.

Topological phases and their entanglement properties:

In the 20th-century physics, the Landau theory of phase transitions based on symmetry and its breakdown was a great success. On the other hand, it has been gradually recognized since the late 1980s that there are a class of disordered “phases” typified by the (integer or fractional) quantum Hall states and quantum spin liquids that cannot be understood within the Landau paradigm. It is now known that in order to characterize those phases we need to use, instead of local order parameters which play a central role in the Laudau framework, various topological invariants or information that see only global (topological) properties of the system (e.g., whether it is spherical or toric) in question. Such states of matter are called “topological” and are currently one of the central topics in condensed-matter physics. Recently, people found that another important concept named “quantum entanglement” that evolved in quantum-information science is very well suited to characterize topological phases. With field-theoretical and numerical approaches, which include the mathematics of topology, we study topological phases that emerge in systems of band insulators/semimetals, superconductors, cold gases and quantum spins.

Exotic phases in quantum magnetism:

On top of the electric charge, electrons possess the “spin" degrees of freedom, that defy purely classical explanations and play an important role in understanding magnetism in solids. In a class of insulators called “Mott insulators”, the motion of electrons is suppressed by strong correlation and their low-temperature properties are dictated by the behavior of a macroscopic number of the electron spins (i.e., quantum mechanical magnetic moments) localized in space. In such situations, depending on the crystal structures, the orbital degrees of freedom, etc., quantum-mechanical properties of electrons yield a variety of interactions among those localized moments and this brings about a diversity of magnetic properties and orders. Our goal is to understand such states of matter that a collection of a huge number of quantum-mechanical magnetic moments exhibit by complex approaches. In particular, we are currently interested in exotic (quantum-)disordered states (dubbed quantum spin liquids), that are stabilized as consequences of the interplay between frustration and the quantum-mechanical phases, as well as the behavior of systems in which spin and additional degrees of freedom (e.g., orbital) are intimately entangled.

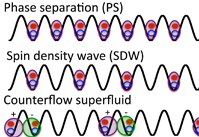
Novel quantum states and quantum phase transitions in ultracold atomic gases confined in optical lattices:

In recent years technology for creating and controlling ultracold atomic gases has been rapidly developed. Of particular interest is a system of an optical lattice loaded with ultracold atoms, which mimics electrons in solids. In such an optical-lattice system, one can precisely control various items determining important properties of the system, such as external potentials, density, interactions, lattice geometry, and statistics of particles. This high controllability makes it possible to discover novel effects and phenomena that cannot be realized in conventional condensed matter systems. We explore novel quantum states and quantum phase transitions by using and developing various theoretical methods.