
| スタッフ | 教授 | 佐々 真一 | 教授 | 齊藤 圭司 |
|---|---|---|---|---|
| 准教授 | 金澤 輝代士 | 准教授 | 荒木 武昭 | |
| 助教 | 松本 剛 | 講師 | デヒャント アンドレアス | |
| 助教 | 北村 光 |
私達の研究室では、非線形、非平衡、ゆらぎ、複雑性、情報、統計解析、推定等をキーワードとした幅広い内容の研究が行われています。
|
原子分子の集まりが生物を構成しているのは紛れもない事実である。生物が示す機能が物質科学の概念とどのように関わっているのだろうか。そのためには、微視的な構成要素がたくさん集まって巨視的なシステムをつくるとき、微視的な記述にはない概念や量がマクロなレベルで創発する機構を探索する必要がある。平衡系の場合には、一般的枠組みとして統計力学が確立しているので、創発の理解は統計力学の中の問題になる。ところが、非平衡系の場合には、現象の解明と同時に新しい理論的枠組みの構築が必要になる。例えば、非平衡条件下相共存など、非平衡ゆらぎがもたらす特異な現象をゆらぎの理論、熱力学の拡張理論、数値実験などを使って理論的解析を進めている。また、ゆらぎの世界の解析に情報論的解析が深く関わってきていることが明らかになってきており、様々なタイプの基本的限界を定式化することも近年のテーマのひとつである。
佐々・Dechant(非線形動力学)グループのページへ |
 |
|
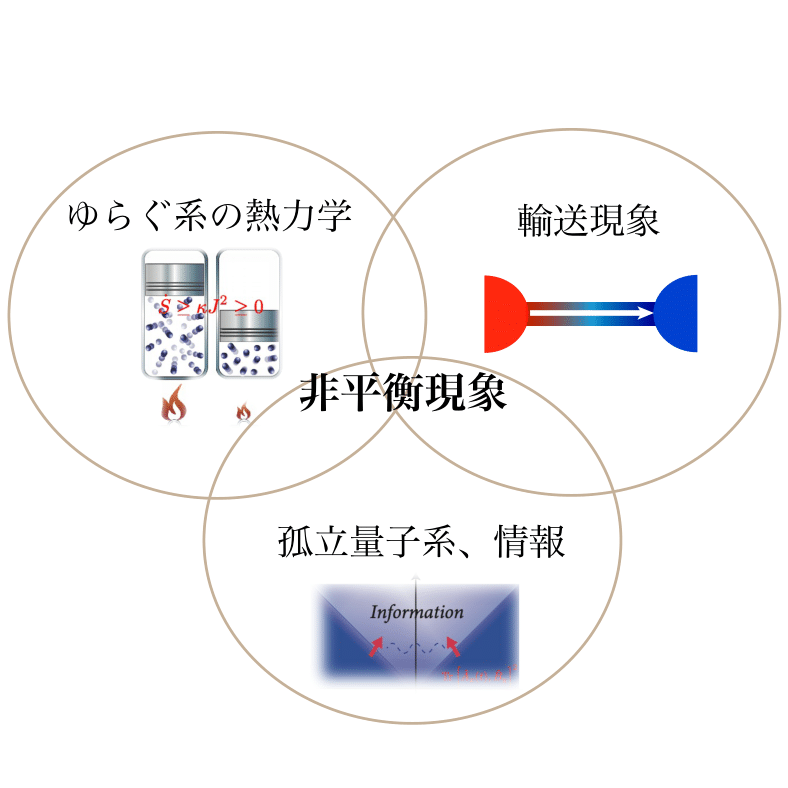
齊藤研究室では、(1)不可逆過程の熱力学、(2)輸送現象の統計力学、(3)量子系での情報伝搬や熱化ダイナミクスなどを研究しています。 自然界には、本質的に出来ないことが存在します。物体は光速以上で移動することは出来ないし、カルノー効率を超えて熱を仕事に変えることは出来ません。自然界の本質である不可逆性は決して元には戻れないという自然界の重要な現象です。齊藤グループでは、不可逆過程の普遍的な性質を探究しています。具体的に、「ゆらぐ系の熱力学」に基づいて非平衡熱力学の様々な熱力学的限界を緻密化する試みや、ミクロとマクロをつなぐ統計力学的な考察などを行っています。また、典型的な非平衡系である、輸送現象の統計力学では、低次元の熱輸送現象や多体系のゆらぐ流体力学による特徴づけなどを行っています。また、量子系においては、量子孤立多体系での熱化現象やエンタングルメント、情報伝播に関する研究を行っています。 齋藤グループのページへ |
 |
|
連続体近似の結果、得られる方程式は多くの場合に非線形の偏微分方程式である。古典力学に従う流体(液体や気体)の方程式であるNavier-Stokes方程式を代表例として、こうした非線形な系の時間的、空間的な変動はとても激しいものになりうる。このため、個々の解の振る舞いには不明な点が多い。天気予報の難しさを思い浮かべてもらえば良い。また、こうした解をたくさん集めて、その統計を考えることも古くから行われているが、激しい変動に起因してガウス分布のような平衡系で見られるものとは全く異なる分布が得られる。現状ではその分布の正確な記述にすら困難がある。このような問題に対して、理論的に新たな突破口を得るべく数値シミュレーションを用いて研究を行っている。
藤・松本(流体物理学)グループのページへ |
 |
|
相転移・相分離の動力学、ソフトマター、複雑流体の物性について理論解析や数値シミュレーションを用いて研究を行っている。ソフトマターは高分子・液晶・コロイドなどの外場に対しソフトな応答を示す系の総称で、物理学・化学・生物学・材料科学の分野にまたがる重要な物質群である。未解明の現象も多く、非線形・非平衡物理の研究の宝庫となっている。電子系の関与する量子非平衡現象や構造不規則物質の数値解析も行っている。実験グループとの共同研究も積極的に進めていきたい。
荒木・北村(相転移動力学)グループのページへ |
 |
|
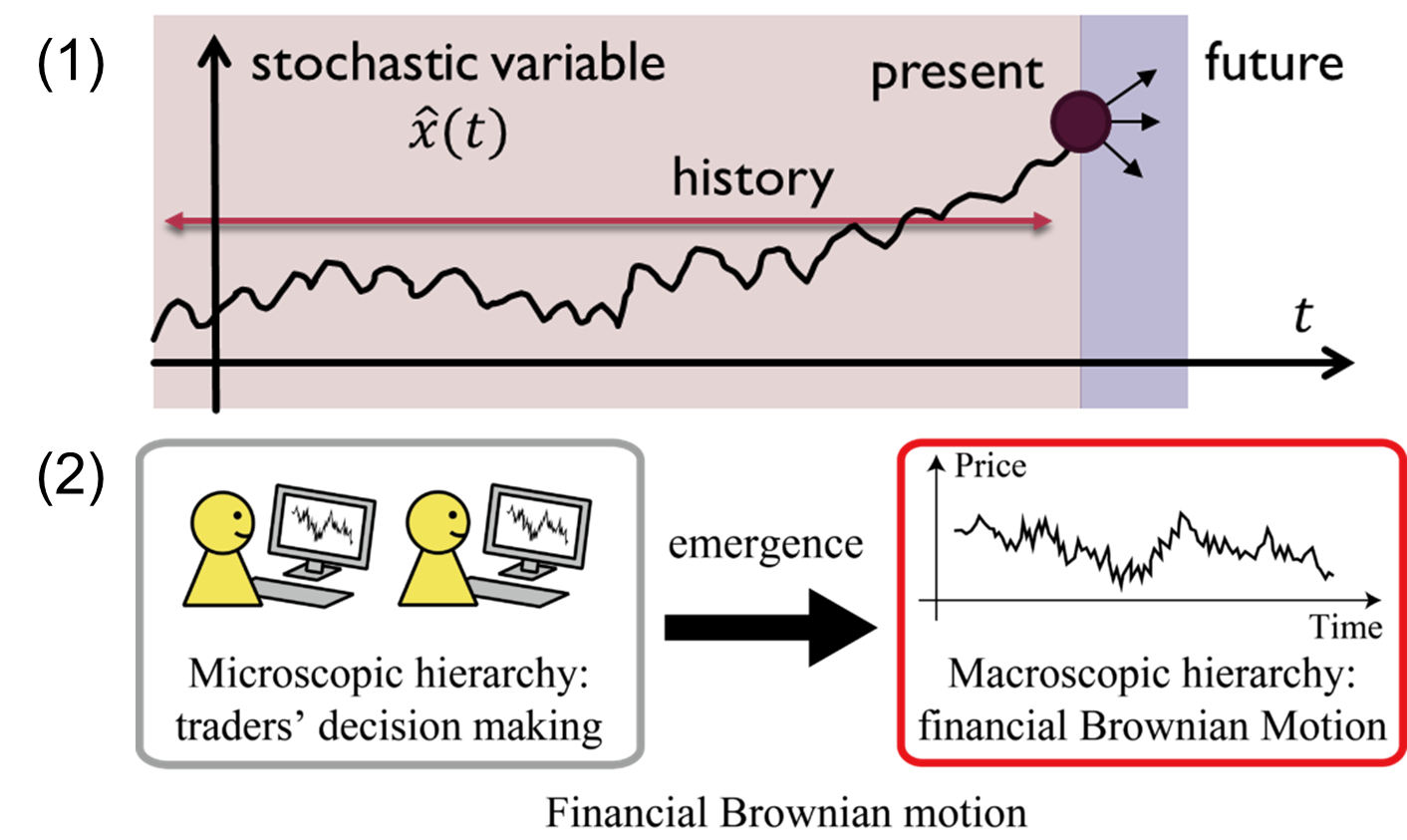
金澤研究室では、(1) 確率過程の理論研究、(2) 経済物理学のデータ解析、ならびに理論研究などを行っています。 (1) 自然・社会現象を記述する道具として確率過程は有用です。最もシンプルな確率過程の理論では、系の過去の履歴に依存しないマルコフ過程を仮定することが多いですが、実際の自然・社会現象ではこの仮定が破れることも多く、過去の履歴に依存する非マルコフ過程が頻繁に現れます。非マルコフ過程は今まであまり理論的には整備されてきませんでしたが、我々は非マルコフ過程の基礎理論研究や、応用としてのデータ解析の研究などを行っています。 (2) また、広い意味での統計物理学の学際分野として金融市場の経済物理学の研究をしています。近年の金融市場では個々のトレーダー単位の行動分析が可能となってきており、ミクロデータ解析に基づいて個々のトレーダーの動力学モデルを帰納的に構築する機運が高まっています。データから構成された多数のトレーダー系に対し、統計物理学の観点から理論的縮約を行うことで、金融市場をミクロからマクロまで体系的に理解することを目指します。 金澤グループのページへ |
 |